EMV: elektromagnetische Verträglichkeit von Geräten
- Kommentare: 1
- Sicher arbeiten
- Artikel als PDF herunterladen

Aufgrund der immer komplexeren und vielfältigeren Form der Datenverarbeitung, -übertragung, Sensorik und Mikroelektronik hat sich eine neue Ingenieursdisziplin gebildet. Diese untersucht die Wechselwirkung elektrischer Geräte im Hinblick auf störende Beeinflussungen, die elektromagnetische Verträglichkeit (EMV).
Warum ist die Prüfung der elektromagnetischen Verträglichkeit notwendig?
Die steigende Notwendigkeit, die Wechselwirkung zwischen Geräten zu prüfen und einzudämmen, ergibt sich aus den folgenden Ursachen:
- Da sich die Forschung und Entwicklung von elektronischen Baugruppen, Apparaten und Systemen in immer höheren Frequenzbereichen bewegt, ist auch die Verkopplung einzelner Bauteile und elektrischer Strukturen miteinander in steigendem Maße zu berücksichtigen.
- Die Forderung nach immer höheren Packungsdichten elektronischer Baugruppen erhöht die Wahrscheinlichkeit auftretender Wechselwirkungen und Störungen zwischen den Elementen dieser Baugruppen.
- Daten werden mit immer geringeren Energien übertragen, was die Störanfälligkeit der Übertragungswege drastisch erhöht.
- Die Erschließung immer neuer Frequenzbereiche in immer dichteren Abständen für die Anwendung in Funk und Datenübertragung führt auch über größere Entfernungen hinweg zu einem steigenden Auftreten unerwünschter Wechselwirkungen zwischen einzelnen Apparaten, Systemen und Anlagen.
Welche Arten von Störungen können auftreten?
Elektromagnetische Beeinflussungen können in Form von reversiblen und irreversiblen Störungen auftreten. Während die reversiblen Störungen lediglich eine Beeinflussung der augenblicklichen Funktion von Geräten darstellen, bedeuten irreversible Störungen die Zerstörung von Bauteilen oder dem Gerät selbst.
Reversible Störungen
Typische Beispiele für reversible Störungen sind:
- Das Übersprechen in der Telefonleitung: Durch unerwünschte Signalübertragung zwischen Telefonleitungen können störende Signale in das Gespräch eingespeist werden.
- Knackgeräusche im Radio, die beim Schalten von Haushaltsgeräten auftreten können.
- Störung der Bildqualität auf Bildschirmen durch hohe Magnetfelder.
Irreversible Störungen
Typische Beispiele für irreversible Störungen sind:
- die Zerstörung elektrischer Komponenten durch elektrostatische Aufladungen
- Überspannungen bei Blitzeinwirkungen
EMV schon bei der Herstellung berücksichtigen
Das Ziel des Entwicklungsingenieurs ist, die elektromagnetischen Beeinflussungen zwischen Geräten, Systemen oder Lebewesen so gering zu halten, dass diese in ihrer Funktionalität nicht eingeschränkt werden.
Die Einschränkung der Beeinflussungen ist auch vom Gesetz (EMVG: Gesetz über die elektromagnetische Verträglichkeit von Geräten) gefordert. So wie die Emission von Lärm, Abwasser und Abgasen gesetzlich mit Auflagen versehen ist, so werden auch den Firmen, die elektrische Geräte vertreiben, im Rahmen der Produkthaftung konkrete Auflagen und Grenzwerte gesetzt, nach denen die produzierten Geräte in Bezug auf andere Geräte oder Lebewesen in einem bestimmten Maß elektromagnetisch verträglich sind.
Das bedeutet einerseits, dass die betrachtete elektrische Einrichtung gegenüber ihrer Umgebung unempfindlich genug ist, um nicht selbst in ihrer Funktion beeinträchtigt zu werden und andererseits, dass die elektrische Einrichtung andere Einrichtungen oder Lebewesen nicht beeinträchtigt. Diese Betrachtung muss jedoch neuerdings erweitert werden, da nicht nur mehr einzelne Geräte in Bezug auf ihre Umgebung betrachtet werden. Heute werden meist verschiedene Einrichtungen als Gesamtheit und deren komplexe Wechselwirkung untereinander betrachtet.
Downloadtipps der Redaktion
Downloadpaket für ortsveränderliche elektrische Arbeitsmittel
Hier gelangen Sie zum Download.
E-Book: Prüfprotokolle für die Elektrofachkraft
Hier gelangen Sie zum Download.
e+-Artikel: Die DGUV Information 203-071: Wiederkehrende Prüfungen elektrischer Anlagen und Betriebsmittel
Grundlegende Begriffe und Zusammenhänge der elektromagnetischen Verträglichkeit
Im Folgenden werden einige grundlegende Begriffe und Zusammenhänge dargestellt, die auf dem Gebiet der EMV wichtig sind. Die in der EMV verwendeten Begriffe sind oft bereits in der Gesetzgebung des EMVG (Gesetz über die elektromagnetische Verträglichkeit von Geräten) festgelegt. So wird z.B. zwischen Geräten, Systemen und Anlagen unterschieden:
Geräte sind alle elektrischen und elektronischen Apparate, Systeme und Anlagen, die elektrische oder elektronische Bauteile enthalten. Die unter das EMV-Gesetz fallenden Geräte müssen so beschaffen sein, dass die Erzeugung elektromagnetischer Störungen begrenzt wird und die Geräte eine angemessene Festigkeit gegen elektromagnetische Störungen aufweisen, sodass ein bestimmungsgemäßer Betrieb möglich ist.
Ein System wird definiert als mehrere zu einem bestimmten Zweck verbundene Apparate, die als einzige Funktionseinheit in Verkehr gebracht wurden (z.B. Stereoanlage mit Empfänger, CD-Player und Kassettendeck).
Eine Anlage ist eine Zusammenschaltung von Apparaten und Systemen oder Bauteilen an einem gegebenen Ort derart, dass diese Bestandteile miteinander eine bestimmte Aufgabe erfüllen.
Ein elektronisches Gerät stellt also den Überbegriff für einen einzelnen Apparat, ein System verschiedener Apparate oder eine Anlage verschiedener Systeme dar. Das bedeutet, dass in einem Gerät immer eine Beeinflussung von internen Elementen des Geräts sowie eine externe Beeinflussung verschiedener Geräte stattfinden kann.
In Bezug auf elektromagnetische Störungen kann ein Gerät also immer durch das Modell in Abbildung 1 dargestellt werden.
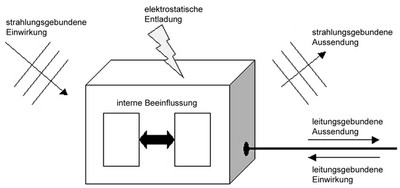
Die interne Beeinflussung stellt in der Regel die unerwünschte Kopplung von Bauteilen oder Gerätemodulen dar. Die externe Beeinflussung wird gebildet durch
- strahlungsgebundene Einwirkung und Aussendung elektromagnetischer Wellen (z.B. durch Funkwellen),
- elektromagnetische Entladung am Gerät (z.B. durch geladene Körper oder Blitzschlag) oder
- leitungsgebundene Einwirkung und Aussendung (z.B. Spannungspulse bei Schaltvorgängen).
Weitere, oft verwendete Begriffe in der EMV sind durch die Bezeichnungen Störquelle bzw. Sender, Störsenke bzw. Empfänger und Kopplungsmechanismus gegeben.
Sender sind auf dem Gebiet der EMV die Geräte, die ein Störsignal aussenden. Sie sind also Störquellen.
Empfänger sind die Geräte, die diese Störsignale empfangen und darauf in ihrem Betriebsverhalten beeinflusst werden. Man bezeichnet diese Empfänger daraufhin als Störsenke.
Über einen Kopplungsmechanismus wird das Störsignal übertragen (siehe Abb. 2). Kopplungsmechanismen in diesem Sinne sind z.B. die elektrische, magnetische oder elektromagnetische Feldkopplung sowie die Kopplung über Leitungen und über die Masse.

Tipp der Redaktion

Sie wollen mehr Infos zu diesem und weiteren Themen?
Dann empfehlen wir Ihnen elektrofachkraft.de – Das Magazin:
- spannende Expertenbeiträge zu aktuellen Themen
- Download-Flat mit Prüflisten, Checklisten, Arbeits- und Betriebsanweisungen.
Auch als Onlineversion erhältlich. Machen Sie mit beim Papiersparen.
Welche Kopplungsmechanismen gibt es?
Auf dem Gebiet der EMV unterscheidet man vier wesentliche Kopplungsmechanismen zwischen Geräten:
- Galvanische Kopplung kann auftreten, wenn zwei Geräte über eine Leitung miteinander verbunden sind. Haben die Geräte durch die Verbindung eine gemeinsame Impedanz, so wirkt diese Impedanz als Übertragungsweg. Die Spannung des einen Geräts an der gemeinsamen Impedanz ist dann vom Strom des anderen Geräts abhängig, der durch diese Impedanz fließt.
- Die kapazitive Kopplung ist dann möglich, wenn zwei Geräte oder deren Zuleitungen geringen Abstand (im Vergleich zur Wellenlänge der Signale) haben. Das elektrische Feld zwischen den Geräten oder Zuleitungen dient dann als Übertragungsweg.
- Die induktive Kopplung ist ebenfalls dann möglich, wenn zwei Geräte oder deren Zuleitungen geringen Abstand (im Vergleich zur Wellenlänge der Signale) haben. Hier dient das magnetische Feld als Übertragungsweg für die Geräte oder deren Zuleitungen.
Die kapazitive und induktive Kopplung über quasistatische Felder tritt nur bei Geräteanordnungen auf, deren Abmessungen deutlich unterhalb der Wellenlänge der Störsignale liegen. Haben Geräte zwar geringen Abstand zueinander, sind jedoch selbst groß gegenüber der Wellenlänge, so ist die elektromagnetische Kopplung im Nahfeld zu betrachten. Hier sind die Geräte über ein elektromagnetisches Feld verkoppelt.
- Die elektromagnetische Kopplung im Fernfeld ist dann zu beachten, wenn Geräte, deren Abmessungen im Bereich oder oberhalb der Wellenlänge liegen, einen weiten Abstand voneinander haben. In diesem Fall kann man auch von Strahlungskopplung sprechen.
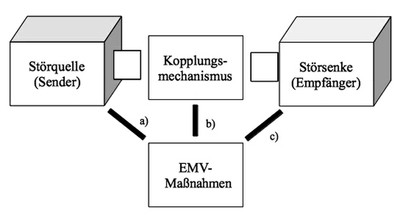
EMV-Maßnahmen
Die elektromagnetische Beeinflussung kann mithilfe verschiedener EMV-Maßnahmen eingedämmt oder verhindert werden (Abb. 3). Die Maßnahmen können nach ihrem jeweiligen Angriffspunkt unterschieden werden:
a) Maßnahmen, die die Emissionen der Störquelle eindämmen
b) Maßnahmen, die den Kopplungsmechanismus unterbrechen (z.B. durch selektive Unterbrechung des Signalpfads)
c) Maßnahmen, die die Störfestigkeit der Störsenke heraufsetzen
Das heißt, das Gerät wird gegen die Störung unempfindlich gemacht (z.B. durch Schirmung).
Beitrag von 2013, geprüft und aktualisiert 2023




















Kommentare
Kommentar von Zülow |
Ich habe seit Februar unterbrechungen der Telefonleitung.Die Telefonleitung ist o.k.Kann ein Elektriker den Störverursacher messen.M.F.G Jörg
Einen Kommentar schreiben